MASCHINELLES LERNEN VISUALISIERT
ROC-Kurve und Gini-Koeffizient
Die Grundlagen
Kurz erklärt
Die „ROC-Kurve“ (ROC = Receiver Operating Characteristic) dient zur Messung der Leistungsfähigkeit eines maschinellen Lernverfahrens bzw. eines jeden Prognoseverfahrens, welches Dinge in zwei Klassen A und B (z. B. blau und rot) einteilt. Die Idee beruht darauf, dass das Verfahren einen kontinuierlichen Output-Wert ausgibt, wobei alle Output-Werte unterhalb eines Schwellenwertes als A (blau) und ansonsten als B (rot) betrachtet werden. Das Verfahren ist dann umso leistungsfähiger, je mehr Punkte eines Testdatensatzes mit bekannten Klassen (blaue und rote Punkte) korrekt klassifiziert werden. Was nichts anderes bedeutet als: die Output-Werte für die blauen Punkte sollten am besten alle unterhalb und die der roten oberhalb des Schwellenwertes liegen.
Sortiert man also alle Punkte des Testdatensatzes von links nach rechts nach aufsteigendem Output-Wert, dann sollten idealerweise alle blauen links und alle roten rechts liegen. Nun kann ich für jeden möglichen Schwellenwert fragen, wie viel Prozent der blauen Punkte links von ihm korrekterweise als blau (True Positive Rate oder Sensitivität) und wie viel Prozent der roten Punkte links von ihm fälschlicher als blau (False Positive Rate oder Spezifität) eingestuft werden. Diese beiden Zahlen kann ich als x- bzw. y-Koordinate eines Punktes nehmen und in ein Quadrat der Seitenlänge 1 (= 100%) zeichnen. Wenn ich dies für jeden möglichen Schwellenwert mache, dann setzen sich diese Punkt zu einer Kurve zusammen – die ROC-Kurve.
Je stärker die ROC-Kurve sich in den oberen linken Bereich des Quadrats erstreckt, desto besser die Performance des Verfahrens. Dies lässt sich in einer Zahl ausdrücken: der Fläche unter der Kurve (Area Under Curve – AUC) oder alternativ mit dem Gini-Koeffizienten, der sich über die Formel 2 * AUC -1 ergibt. Dieser nimmt Werte zwischen -100 % und +100 % an. Ein positiver Gini-Koeffizient bedeutet, dass das Verfahren korrekt trennt – je höher, desto besser. Ein negativer Gini-Koeffizient bedeutet, dass das Verfahren ebenfalls trennt, allerdings genau falschherum (rote werden als blau, blaue als rot klassifiziert). Ein Gini-Wert nahe 0 bedeutet, dass das Verfahren nicht besser trennt als eine zufällige Zuordnung (Münzwurf).
Was kann ich tun?
Anleitung
Im oberen Band sind beispielhaft die Punkte eines Testdatensatzes (mit bekannten Klassen – blau oder rot) von links nach rechts aufsteigend nach den Output-Werten eines fiktiven Prognoseverfahrens (egal, welcher Art) sortiert. In der Grafik unten sehen Sie die zugehörige ROC-Kurve und den Gini-Koeffizienten. Im oberen Band können Sie Datenpunkte mit der Maus verschieben, löschen (nach unten links aus dem Bild ziehen) oder neu hinzufügen (Buttons rechts) und dabei insbesondere die Links-Rechts- Sortierung ändern. Bei jeder solchen Veränderung wird die ROC-Kurve und der Gini-Koeffizient neu berechnet. Bei perfekter Sortierung (alle blauen links, alle roten rechts) erreichen wir einen Gini-Wert von 100%. Bei perfekter falscher Sortierung (alle blauen rechts, alle roten links) ergibt sich ein Gini-Wert von -100%,
Während Sie einen Punkt verschieben, wird dessen horizontale Position als Schwellenwert interpretiert, der zwischen blau (links) und rot (rechts) trennt. Dabei wird vermerkt, welche True Positive Rate bzw. welche False Positive Rate sich für diesen Schwellenwert ergeben; der entsprechende Punkt auf der ROC-Kurve wird weiß angezeigt.
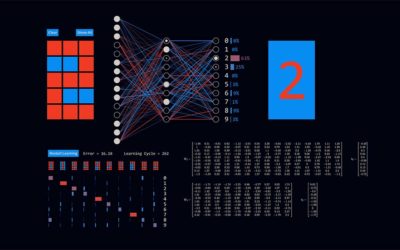
Handschrifterkennung mit Neuronalen Netzen
Die App visualisiert ein einfaches neuronales Netz – wie es lernt und wie es arbeitet – am Beispiel der Erkennung handgeschriebener Ziffern. Diese können mit der Maus live auf ein einfaches Zeichenfeld bestehend aus 5 x 3 Pixeln geschrieben werden. Die geschriebene Ziffer wird vom neuronalen Netz dabei unmittelbar in die erkannte Ziffer übersetzt. Wie gut das gelingt, hängt davon ab, wie gut das neuronale Netz trainiert ist.
kNN dreidimensional
Der kNN-Algorithmus in drei Dimensionen als „künstlerische“ Darstellung zum Drehen, Zoomen und Verstehen.
Stein, Schere, Papier mit kNN
Der kNN-Algorithmus ist ein einfacher und wirkungsvoller Machine-Learning-Algorithmus für Klassifikations- und Regressionsaufgaben. Hier im Beispiel kann man ihn live erleben, wie er Handpositionen als Stein, Schere oder Papier klassifiziert, nachdem man ihn mit entsprechenden Schnappschüssen trainiert hat.
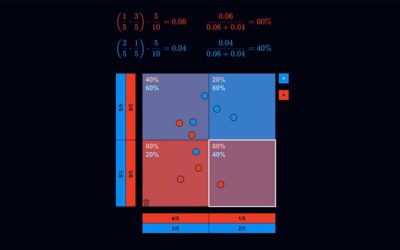
Naive Bayes
Der Naive-Bayes-Algorithmus ist ein Machine-Learning-Algorithmus. Er wird zum Beispiel in Spam-Filtern von E-Mail-Programmen verwendet. Die VisuApp illustriert die dahinterstehende Logik an einem Beispiel:
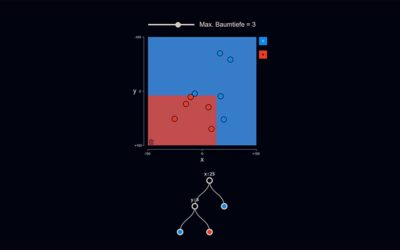
Entscheidungsbaum
Entscheidungsbäume sind maschinelle Lernverfahren, die sich durch besonders gute Verständlichkeit auszeichnen, da der Weg vom Input zum Ergebnis Schritt für Schritt nachvollzogen werden kann. In der VisuApp wird ein Entscheidungsbaum auf Basis von Trainingsdaten trainiert und grafisch dargestellt.
Random Forest
Random Forests sind maschinelle Lernverfahren, die auch als „Ensemble-Verfahren“ bezeichnet werden. Hierbei wird statt nur eines einzelnen Entscheidungsbaums eine ganze Gruppe solcher Bäume trainiert („Wald“). Zur Klassifikation einer Eingabe wird diese in jedem Baum ausgewertet. Diejenige Klasse, die am häufigsten gewählt wurde, ist die Ausgabe des Random Forest.
Lineare Regression
Die klassische lineare Regression kann wahrscheinlich als das einfachste maschinelle Lernverfahren betrachtet werden. Jedoch ist das Verfahren auch sehr „starr“ in dem Sinne, dass es nur lineare (d. h. geradlinige) Entscheidungsgrenzen zulässt.
Der kNN-Algorithmus
Der K-Nearest-Neighbours-Algorithmus ist ein einfacher und intuitiver Machine-Learning-Algorithmus, den wir mittels einer interaktiven VisuApp veranschaulichen.
Support Vector Machines
Support Vector Machines stellen eine der leistungsfähigsten und am weitesten verbreiteten Kategorien von maschinellen Lernverfahren dar.